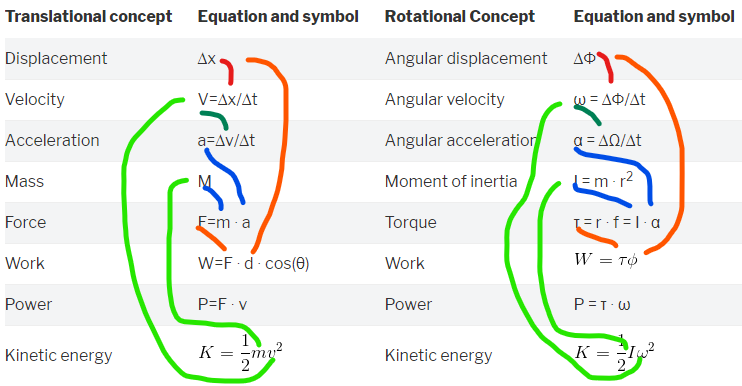
Friday’s post includes the translational concepts we have studied, as well as the rotational equivalents. If you were absent, be sure to check this page.
Today
- Read and takes notes on Section 7.1; pages 189-192. Turn in your notes for credit.
- Work on all odd-numbered problems on page 218-219, numbers 1-13. Show all your work, and show both the SAE (inches, miles, etc.) and metric values when presented with SAE values (OK to use your phone for conversions).
- Complete all problems for homework.
Remember you can check the answers to the odd-numbered problem in the back of the book, or the scanned versions here.