Contents of this post
Teeter totters and torque
Torque
- Introduction to Torque in your textbook (skim pages 226-230)
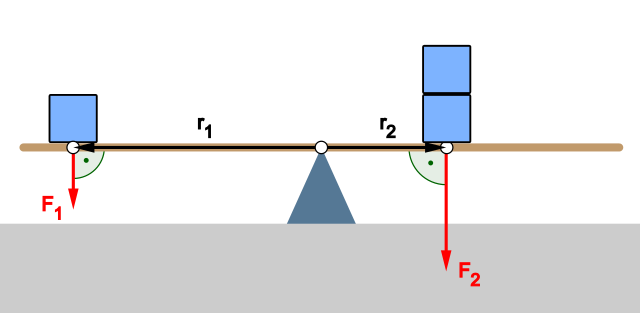
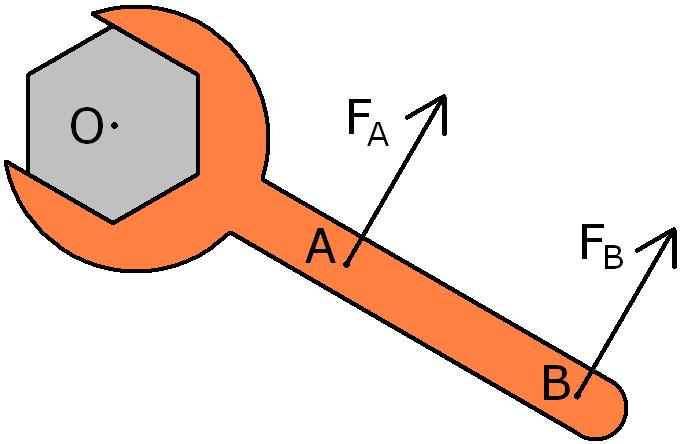
Torque is the rotational analog of force. Torque is calculated as the product of the force and the distance from the center.
$latex \vec{\tau }=\vec{r}\cdot \vec{F}$
This is very similar to our $latex \vec{\ W }=\vec{d}\cdot \vec{F}$, to which we needed to add cosine for forces that aren’t in the same direction as the motion: $latex \vec{\ W }=\vec{d}\cdot \vec{F} cos(\theta )$ . We need to do the same for torque, although in this case we need to use sine (since torque is maximum when the force and radius are perpendicular to each other), so we end up with:
$latex \vec{\tau }=\vec{r}\cdot \vec{F}sin(\theta)$
Caution: While the units of Nm, which are the same for work, torque is not energy. It is more similar to force: A net force acting on an object will cause that object to accelerate. A net torque acting on an object will cause that object to undergo rotational acceleration.
Introduction to torque video
With Billy, Bo, and Bobby
Doorknob placement variations

Which door provides you with the most torque?
