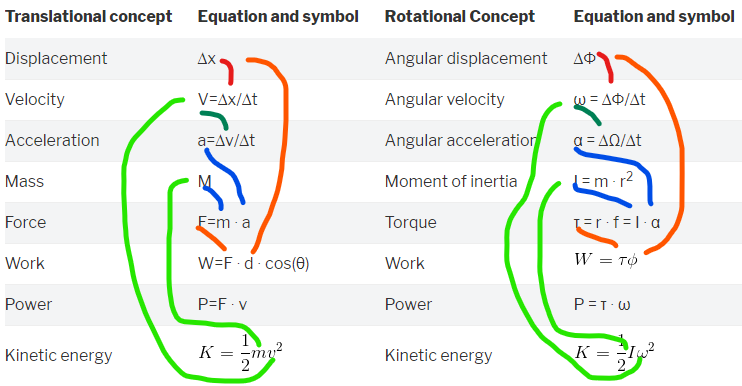
In our next unit we will be studying rotational motion. So far, the motion we have been studying is translational–where object move from one place to another. In rotational motion, things go around in circles, but the system doesn’t move from one place to another.
Comparing translational and rotational motion.
Greek letters used above
You need to be able to use the name for these Greek letters
- Φ phi (lower case)
- ω omega (lower case)
- α alpha (lower case)
- Ι iota (upper case)
- τ tau (lower case)